Библиотеки и данные
# Понадобится для чтения и записи аудио файлов from scipy.io import wavfile # Это нужно для проигрывания аудио файлов прямо в блокноте from IPython.display import Audio # А это набор для задачи import numpy as np import matplotlib.pyplot as plt from sklearn.decomposition import PCA
# Скачаем данные ! wget https://www.dropbox.com/s/p5147nr8mzemxnr/Beethoven_Violin_Sonata_Op_96_first_movement_bars_1-22.wav
# Прочитаем аудио дорожку при помощи wavfile
samplerate, data = wavfile.read('Beethoven_Violin_Sonata_Op_96_first_movement_bars_1-22.wav')
Анализ данных
Samplerate есть частота дискретизации — стандартное для аудио значение — 44100 Гц.
Частота дискретизации говорит о том, сколько последовательных элементов массива с сигналом кодируют звук длительностью 1 секунда.
# Посмотрим какая у нас частота дискретизации print(samplerate) Вывод: 44100
# Если поделить длину массива сигнала на samplerate, получится длительность аудиодорожки в секундах print(len(data) / samplerate) # 45 секунд - похоже на правду:) Вывод:45.139591836734695
# Заметим, что звук - стерео, так как сигнал кодируется двумя каналами (для левого и правого динамика): print(data.shape) Вывод:(1990656, 2)
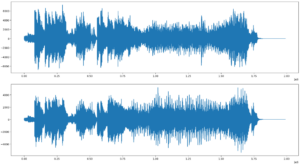
# Отрисуем сигналы в обоих каналах # Канал 1 plt.figure(figsize=(20,5)) plt.plot(data[:,0]) plt.show() # Канал 2 plt.figure(figsize=(20,5)) plt.plot(data[:,1]) plt.show()
Вывод:
# Усредним каналы, и получим моно звук, с которым будет проще работать mono_sound = np.mean(data, axis=1) print(mono_sound.shape) Вывод:(1990656,)
# Давайте послушаем наконец, что же мы будем сжимать:) Audio(mono_sound, rate = samplerate)
# Для удобства - обрежем массив с сигналом так, чтобы его было удобнее делить на равные части, датасет из которых и необходимо будет сжать известными методами. mono_sound_to_cut = mono_sound[:1990000]
# Проверим, что наш звук теперь это просто вектор чисел print(mono_sound_to_cut.shape) Вывод: (1990000,)
Разделим сигнал на равные части (длину каждой части возьмем равной 1000) и соберем из них «датасет», который будет представлять из себя двухмерный массив — «матрицу», в которой каждая часть сигнала длины 1000 находится в отдельной строке).
То есть первая часть содержит первые 1000 чисел сигнала и находится в первой строке матрицы, вторая часть следующие 1000 чисел сигнала и находится во второй строке матрицы и так далее.
mono_sound_to_cut = np.reshape(mono_sound_to_cut, (1990, 1000))
mono_sound_to_cut
Вывод:
array([[ 0. , -1. , -1. , ..., 88.5, 58.5, 18. ],
[-25.5, -61.5, -81.5, ..., 30.5, -20.5, -53. ],
[-67.5, -65.5, -50. , ..., 118.5, 118.5, 86.5],
...,
Переводем "матрицу" обратно в звуковой сигнал, то есть развернем данные обратно из матрицы размера(число объектов, 1000)в вектор длины(число объектов * 1000). Проверим, что все работает верно, путем воспроизведения "восстановленного" сигнала -- он должен совпасть в точности с изначальным (ведь им на самом деле и является).
Применение алгоритма
Выполним PCA преобразование нашей матрицы, и получим данные, сжатые в пространство меньшей размерности.
На этом этапе у нас есть наш «датасет» с 1000 «признаками» и мы хотим уменьшить число «признаков» путем применения метода PCA. Число компонент для начала не стоит брать слишком маленькое число, чтобы потом было проще понять, в случае плохого результата — компонент оказалось недостаточно или где-то ошиблись.
from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler print(mono_sound_to_cut.shape) # Scale data before applying PCA scaling=StandardScaler() #Use fit and transform method scaling.fit(mono_sound_to_cut) Scaled_data=scaling.transform(mono_sound_to_cut) # Set the n_components=1000 principal=PCA(n_components=1000) principal.fit(Scaled_data) x=principal.transform(Scaled_data) # Check the dimensions of data after PCA print(x.shape) Вывод: (1990, 1000) (1990, 1000)
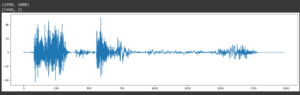
Построим две главные компоненты в наглядной форме.
То есть необходимо применить метод PCA к нашей матрице с числом компонент, равным 2 (тем самым получив датасет с 2 «признаками»). Это позволит нам отрисовать данные на плоскости, чтобы попытаться уловить зависимости.
print(mono_sound_to_cut.shape) # Scale data before applying PCA scaling=StandardScaler() #Use fit and transform method scaling.fit(mono_sound_to_cut) Scaled_data=scaling.transform(mono_sound_to_cut) # Set the n_components=2 principal=PCA(n_components=2) principal.fit(Scaled_data) x=principal.transform(Scaled_data) # Check the dimensions of data after PCA print(x.shape) # Отрисуем plt.figure(figsize=(20,5)) plt.plot(x[:,0]) plt.show()
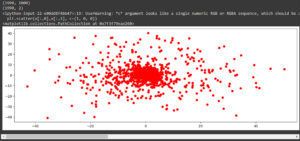
Постройте scatter plot датасета в пространстве первых двух компонент, а третью используйте как цвет. То есть необходимо применить метод PCA уже с 3 компонентами и нарисовать опять точки, только передав третью компоненту в качестве цвета.
print(mono_sound_to_cut.shape) # Scale data before applying PCA scaling=StandardScaler() #Use fit and transform method scaling.fit(mono_sound_to_cut) Scaled_data=scaling.transform(mono_sound_to_cut) # Set the n_components=2 principal=PCA(n_components=2) principal.fit(Scaled_data) x=principal.transform(Scaled_data) # Check the dimensions of data after PCA print(x.shape) plt.figure(figsize=(15, 5)) plt.scatter(x[:,0],x[:,1], c=(1, 0, 0))
Нам осталось заняться непосредственно «сжатием» звука и проверкой правильности наших действий.
Выполним обратное PCA преобразование сжатых данных и получим «матрицу» с сжатым звуком.
Воспользуемся обратным преобразованием PCA (inverse_transform), чтобы из матрицы размера (число объектов, число компонент) перейти в матрицу размера (число объектов, 1000).
print(x.shape) new_data = principal.inverse_transform(x) print(new_data.shape) Вывод: (1990, 2) (1990, 1000)
# сильно ужатый звук стал шумом
result_restore = np.reshape(new_data, (1990000))
print(result_restore.shape)
Audio(result_restore, rate = samplerate)
Исследуем зависимость качества звука от числа компонент. Подберем «на слух» минимальное число компонент, при котором звук практически не отличается от оригинала.
# Scale data before applying PCA scaling=StandardScaler() #Use fit and transform method scaling.fit(mono_sound_to_cut) Scaled_data=scaling.transform(mono_sound_to_cut) # Set the n_components=100 principal=PCA(n_components=100) principal.fit(Scaled_data) x=principal.transform(Scaled_data) # Check the dimensions of data after PCA print(x.shape) new_data = principal.inverse_transform(x) print(new_data.shape) result_restore = np.reshape(new_data, (1990000)) print(result_restore.shape) Audio(result_restore, rate = samplerate)
print("Исходное МОНО")
Audio(mono_sound, rate = samplerate)
Попробуем отфильтровать сигнал с помощью функции gaussian_filter1d из scipy.ndimage. Это поможет убрать неприятный дробовой шум при сильном сжатии
from scipy.ndimage import gaussian_filter1d Audio(gaussian_filter1d(result_restore, 2), rate = samplerate)